Input
CaDeX
Motion2VecSets
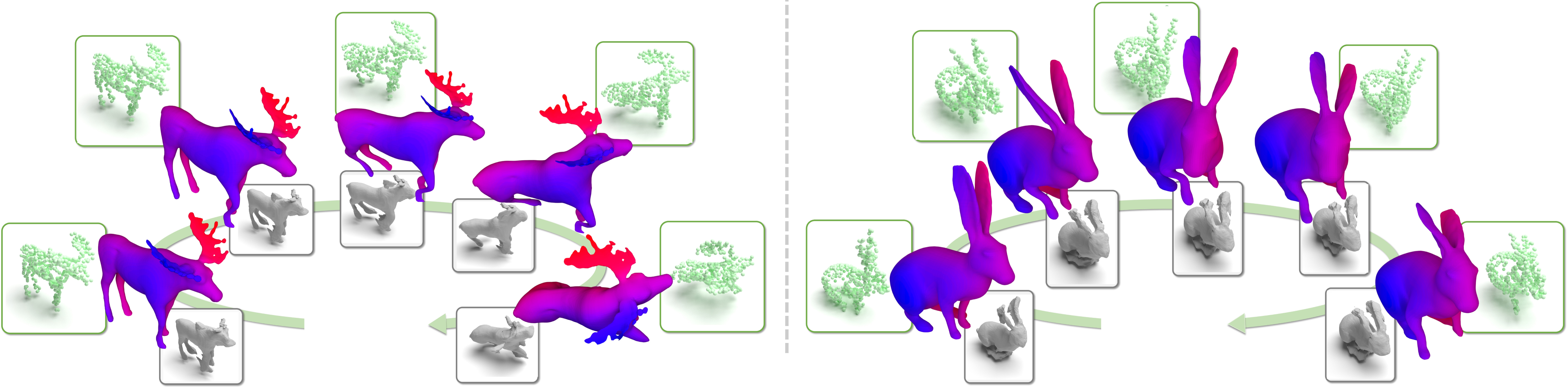
We introduce Motion2VecSets, a 4D diffusion model for dynamic surface reconstruction from point cloud sequences. While existing state-of-the-art methods have demonstrated success in reconstructing non-rigid objects using neural field representations, conventional feed-forward networks encounter challenges with ambiguous observations from noisy, partial, or sparse point clouds. To address these challenges, we introduce a diffusion model that explicitly learns the shape and motion distribution of non-rigid objects through an iterative denoising process of compressed latent representations. The diffusion-based prior enables more plausible and probabilistic reconstructions when handling ambiguous inputs. We parameterize 4D dynamics with latent vector sets instead of using a global latent. This novel 4D representation allows us to learn local surface shape and deformation patterns, leading to more accurate non-linear motion capture and significantly improving generalizability to unseen motions and identities. For more temporal-coherent object tracking, we synchronously denoise deformation latent sets and exchange information across multiple frames. To avoid the computational overhead, we design an interleaved space and time attention block to alternately aggregate deformation latents along spatial and temporal domains. Extensive comparisons against the state-of-the-art methods demonstrate the superiority of our Motion2VecSets in 4D reconstruction from various imperfect observations, notably achieving a 19% improvement in Intersection over Union (IoU) compared to CaDex for reconstructing unseen individuals from sparse point clouds on the DeformingThings4D-Animals dataset.
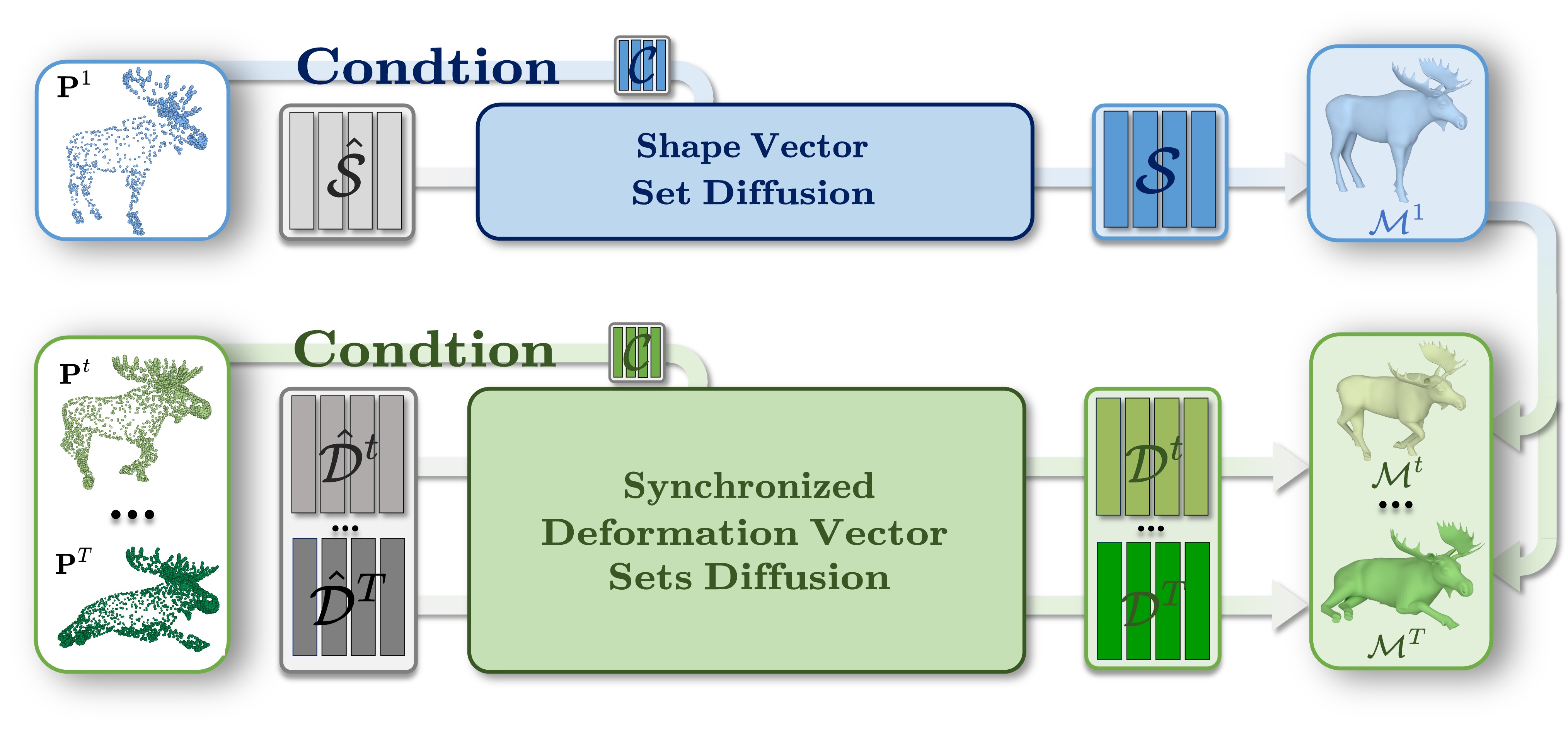
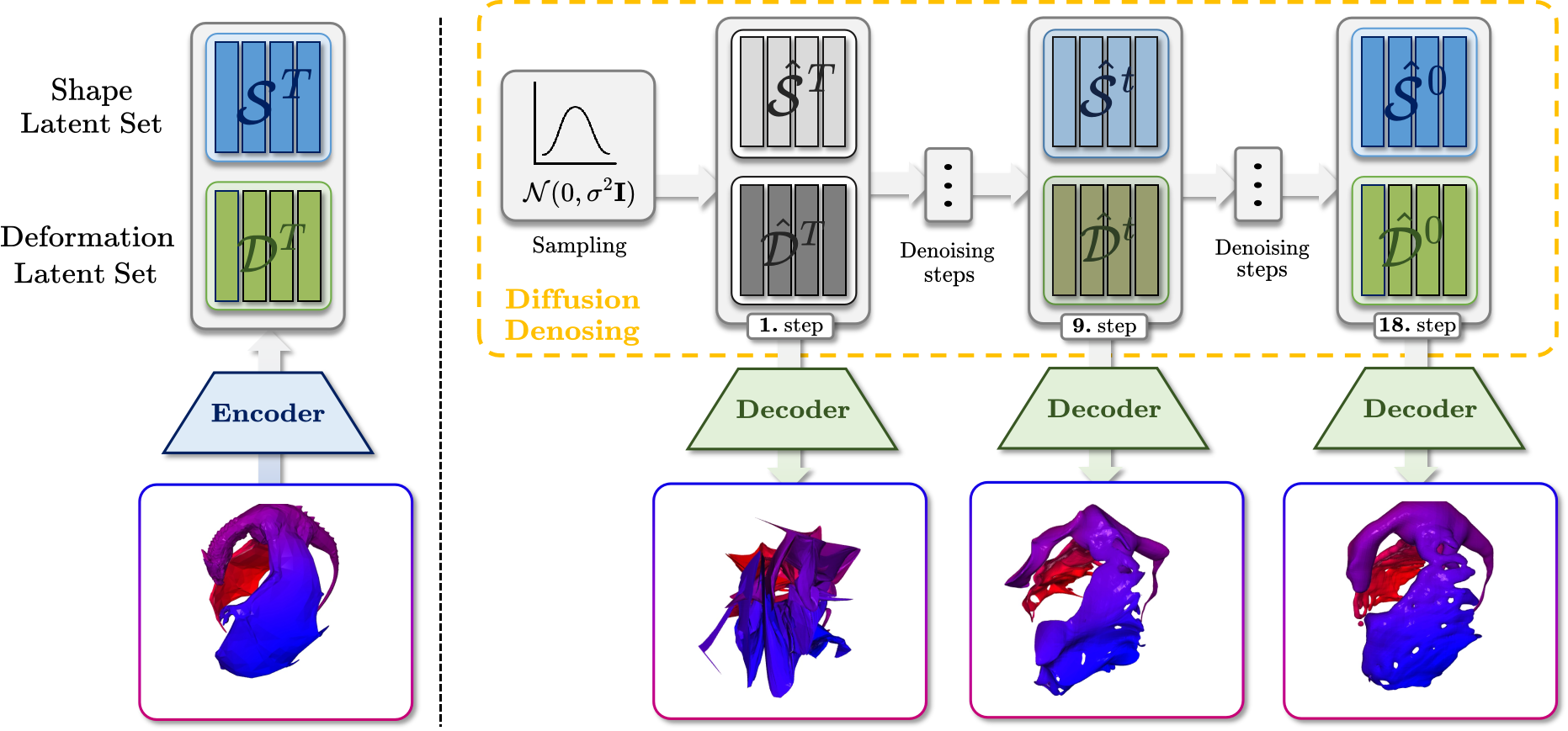
Given a sequence of sparse and noisy point clouds as inputs \(\{\mathbf{P}^t\}_{t=1}^{T}\), Motion2VecSets outputs a continuous mesh sequence \(\{\mathcal{M}^t\}_{t=1}^{T}\). The initial input frame \(\mathbf{P}^1\) (top left) is used as condition in the \(\textcolor[RGB]{0, 32, 96}{\mathbf{Shape\text{ }Vector\text{ }Set\text{ }Diffusion}}\), yielding denoised shape codes \(\mathcal{S}\) for reconstructing the geometry of the reference frame \(\mathcal{M}^1\) (top right). Concurrently, the subsequent input frames \(\{\mathbf{P}^t\}_{t=2}^{T}\) (bottom left) are utilized in the \(\textcolor[RGB]{56, 87, 35}{\mathbf{Synchronized\text{ }Deformation\text{ }Vector\text{ }Sets\text{ }Diffusion}}\) to produce denoised deformation codes \(\{\mathcal{D}^t\}_{t=2}^{T}\), where each latent set \(\mathcal{D}^t\) encodes the deformation from the reference frame \(\mathcal{M}^1\) to each subsequent frame \(\mathcal{M}^t\).
Input OFlow LPDC CaDex Ours
Input OFlow LPDC CaDex Ours
Input
Ours
Input
Ours
@misc{cao2024motion2vecsets,
title={Motion2VecSets: 4D Latent Vector Set Diffusion for Non-rigid Shape Reconstruction and Tracking},
author={Wei Cao and Chang Luo and Biao Zhang and Matthias Nießner and Jiapeng Tang},
year={2024},
eprint={2401.06614},
archivePrefix={arXiv},
primaryClass={cs.CV}
}